Identity Mapping in Deep Residual Networks
이 논문에서 저자는 Residual block의 propagation formulation을 분석했습니다. 또한 Skip connection을 하는 다양한 방식들을 분석했습다. 또한 다양한 activation 방식을 통해서 차이점들을 확인했습니다.
Analysis of Deep Residual Networks.
논문 [1]에서 표현한 Residual Unit은 아래와 같은 수식을 표현할 수 있습니다.
여기서 은 Residual Unit에서 l번째 입력값입니다.
는 l번째 Residual Unit와 연관된 모든 weights와 bias값의 총 집합입니다. 이때 하나의 Residual Unit은 K 겟수의 layer들을 가질수 있습니다.
만약 우리가 function h를 identity mapping 이라고 가정하고 function f 또한 identity mapping 가정한다면, 아래와 같은 수식으로 변환할 수 있습니다.

이 수식을 k = 1 부터 L 제귀적으로 합친다면, 우리는 아래와 같은 수식으로 바꿀 수 있습니다:
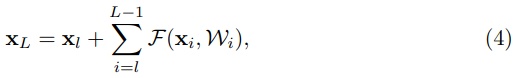
이 수식을 통해서 Residual Network에 관한 여러가지 특성들을 알 수 있습니다.
- 깊은 Residual Unit L은 얕은 Residual unit들과 Residual Functions들의 합으로 표현될 수 있다.
- 어떠한 깊은 unit L은 unit L 전에 있는 모든 residual function의 출력 값들의 합으로 표현할 수 있다.
위의 수식 4 번을 통해서 backpropagation 특성들을 확인 할 수 있습니다. Back propagation 하기 전에 graident equation을 살펴보면 아래와 같습니다.
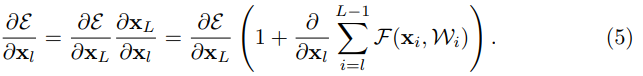
이 수식을 통해서 function F가 -1이 되지 않는 이상, graident는 항상 1 이상을 유지합니다. 그럼으로 gradient vanishing 효과가 나타나지 않습니다.
On the Importance of Identity Skip Connections
위의 분석에서는 function H 값을 identity로 추정한 상태에서의 해석입니다. function h를 로 바꾸어서 identity shortcut을 없엤다면 아래와 같은 수식이 나옵니다.
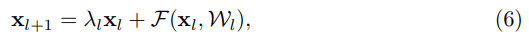
여기서 은 Shortcut을 변환하는 Scalar 값입니다.
이 함수는 수식 4번과 같이 제귀적으로 표현한다면, 아래와 같은 수식이 나오게됩니다.
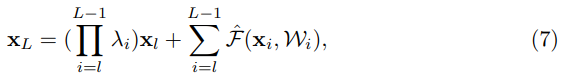
수식 5 번을 구한것처럼 backpropagation equation을 찾아보면 아래와 같이 나옵니다.
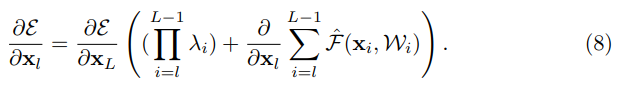
Identity를 사용한 수식 5와는 다르게, 수식 8은 항이 존재합니다. 이때
라면, 저 곱셈항이 기하급수적으로 증가하게 됩니다. 그와 반대로
라면, 기하급수적으로 작아지게 되어 graident vanishing효과가 나타나게 됩니다.
그럼으로 만약 레이어의 수가 증가한다면, shortcut을 사용할 때 추가적은 weight를 집어넣는 것이 weight 값들에게 information propagation을 막고 training을 방해합니다.
Experiment on Skip Connections
위의 수식을 통해서, layer의 수가 증가할수록, identity를 제외한 skip connection 사용시에 training error의 상승하는 문제점이 생깁니다. 그럼으로, 이 논문의 저자는 다양한 shortcut을 통해서 이를 증명하려고 합니다.
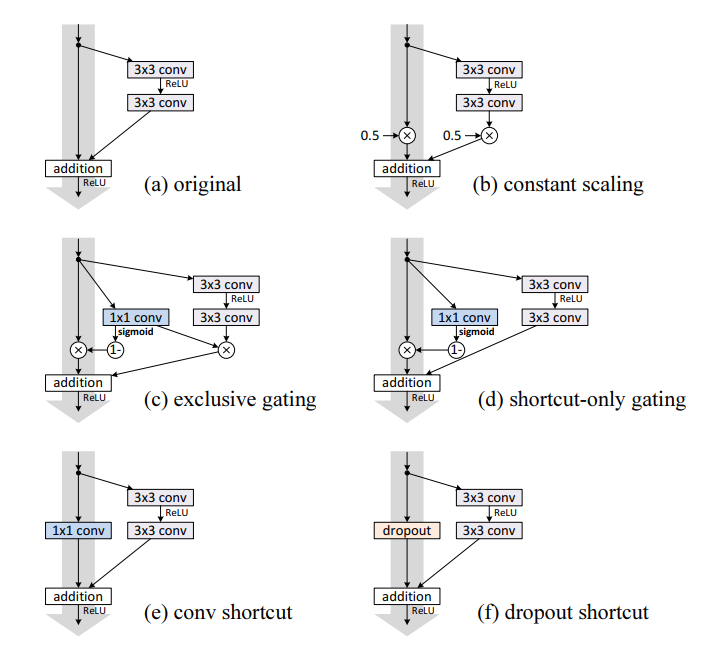
위에 보시는 이미지에서 처럼 다양한 shortcut을 실험합니다. 여기서 a) original은 이전 논문에서 사용한 identity를 의미합니다. b) constant Scaling은 shortcut 이나 Residual function 값에 실수 값을 곱해주는 것을 의미합니다. c) exclusive gating은 Highway Network에서 사용한 gating mechanism을 따른 것입니다. Convolutional network에서 gating function은 convolutional layer에 sigmoid 함수를 적용한 것입니다. 여기서, Shortcut에는
를 residual function에는
를 적용한 것을 의미합니다. d) shortcut-only gating은 c)의 exclusive gating에서 residual function에 적용한 g(x)를 없엔 것입니다. e)의 convolutional shortcut은 [1] 논문에서 적용해보았던 option C를 크게 적용해본것 입니다. f)의 dropout shortcut은 shortcut에 dropout layer를 적용해본 것입니다.
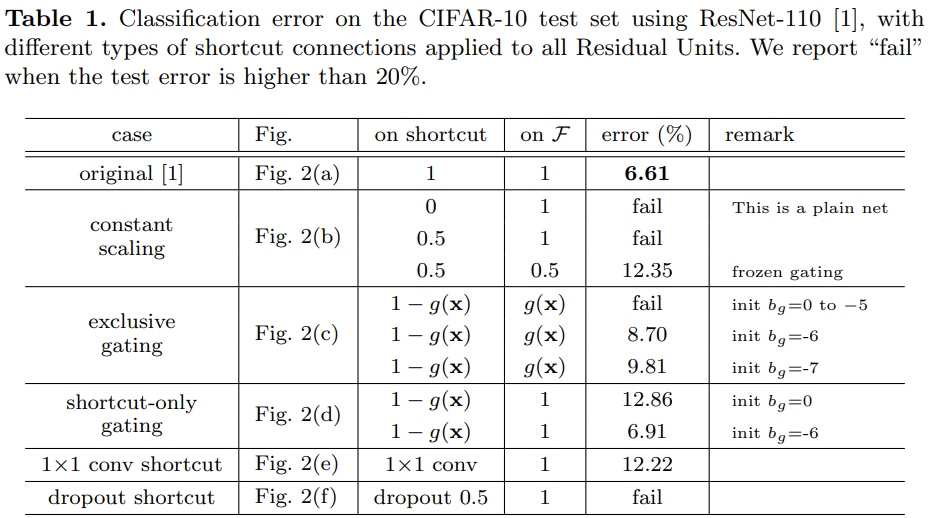
위의 Table 1에서의 결과를 보면, 가장 기본적인 orignal layer가 가장 좋은 결과를 자지고 왔고, 나머지는 이론적으로 계산한것과 비슷하게 shortcut에 weight를 적용할 경우 더 안좋은 결과를 냈습니다.
On the Usage of Activation Function.
위의 실험에서는 SkipConnection의 다양한 방식에 대해서 이야기 해보았다면, 이 아래에는 Activaiton function을 변경시킬 경우 얻을 수 있는 차이점들을 확인해 보는 실험입니다. 이때 Activation function의 종류를 변경하는 것이 아닌 Activation function의 순서를 변경할 때의 차이점을 확인한 것입니다.
Experiment on activation

위의 이미지는 activation 방법에 ResNet 110과 ResNet164를 CIFAR10 데이터를 훈련시킨 결과입니다. 이때 ResNet 110은 두개의 convolutional layers를 사용한 반면, ResNet 164는 두 개의
convolutional layers를
convolutional layer와
convolutional layer, 마지막으로
convolutional layer로 치환한 것입니다..
| ResNet 110 Residual Unit | ResNet 164 Residual Unit |
|---|---|
 |
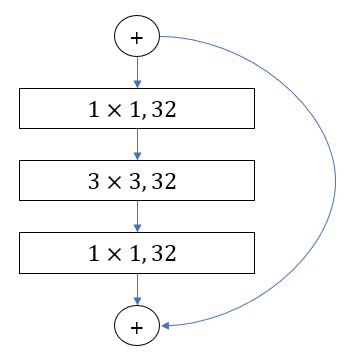 |
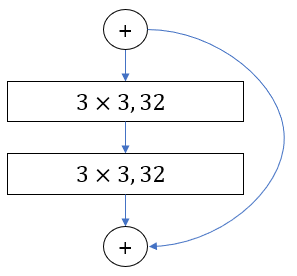
왼쪽 이미지는 ResNet 110의 Residual Unit을 표현한 것이고, 오른쪽 이미지는 ResNet 164의 Residual Unit을 표현한 것입니다. ResNet110과 ResNet 164 모두 18 개의 Residual Unit을 사용했지만, ResNet 164이 3개의 Layers 를 가지고 있기 때문에 2개의 Layer를 가지고 있는 ResNet110과 비교해서 더 많은 레이어를 가지고 있습니다..
위의 이미지에서 확인할 수 있다싶이 Preactivation을 하는 경우 error rate가 줄어든 것을 확인 할수 있습니다.