MobileNets:Efficient Convolutional Neural Networks for Mobile Vision Application

Depthwise separable convolutions를 사용한 간소화된 architecture를 기반으로 MobileNet은 가벼운 DNN을 만드려고 합니다. 이 논문에서 저자는 두가지 global hyperparameter를 소개합니다. 이 두개의 hyperparameter는 효율적으로 정확도와 latency를 교환합니다.

Introduction

AlexNet이 ImageNet Challenge: ILSVRC 2012를 이기고 난 이후, Convolutional Neural Network는 컴퓨터 비전에서 범용적으로 사용되는 기술이 되었습니다. 이 이후로 인공신경망 설계의 전체적인 추세는 깊고 복잡한 신경망을 통해서 높은 정확도를 얻는 것을 목표로 하고 있습니다. 하지만 정확도를 증가시키는 발전은 높은 계산 복잡도를 통해서 이루어지고 있습니다. 실생활 속에서, 예를 들어 로보틱스, 자율주행 자동차, 그리고 증강현실에서, 물체 인식은 빠른시간 내에 계산되어야 합니다.

이 논문에서 저자는 효율적인 신경망 구조와 두개의 hyperparameter를 소개합니다. 이를 통해서 아주 작고 연산 속도가 빠른 모델을 만듭니다. 이는 모바일 기기들과 임베디드 비전 프로그램의 설계 요건에도 맞는 인공신경망 입니다.

Prior Work

작고 효율적인 인공신경망을 만드는 방법은 여러가지가 있습니다. 다양한 방식들은 두가지의 커다란 분류로 나뉠수 있습니다:

미리 훈련된 신경망을 압축하는 방식
작은 인공신경망을 훈련하는 방식

이 논문에서 저자는 새로운 부류의 인공신경망 구조를 제시합니다. 이 구조는 모댈 게발자로 하여금 자신들의 어플리케이션의 자원 제한에 맞는 작은 인공신경망을 고를 수 있게 만들어 줍니다. MobileNet의 가장 기초적인 초점은 레이턴시를 최적화 하는 것은 물론 작은 신경망을 만드는 것입니다.

Training small networks

MobileNet은 depthwise separable convolution에 기반하여 만들어 졌습니다. Depthwise separable convolutiondms Inception 모델에서 첫 몇게의 레이어에서 연산을 줄이기 위해서 사용되었습니다. Flatten Network는 인공신경망을 fully factorized convolution을 기반으로 만들어졌고, extremely factorized network에 대한 가능성을 보여주었습니다. Factorized Networks는 small factorized convoutions와 topological conncetions의 사용을 소개했습니다. Xception Network는 depthwise separable filter를 증가시킴에 따라서 Inception V3 모델을 능가하는 결과를 보여주었습니다. Squeezenet은 bottlenet 방식을 사용해서 아주 작은 신경망을 만들었습니다. 다른 방식으로는 structured transform networks와 deep fried convnet이 있습니다.

작은 신경망을 훈련시키는 또 다른 방식으로는 커다란 인공신경망을 통해서 작은 신경망을 훈련시키는 방식도 있습니다.

Obtaining small networks by factorizing or compressing pretrained networks.

Quantization, hashing, pruing 그리고 vector quantization과 허프만 코딩을 사용하는 압축은 다양한 논문에서 확인 할 수 있습니다. 게다가, 다양한 Factorization은 미리 훈련된 신경망의 연산을 더욱더 빠르게 만들어 줍니다.

MobileNet Architecture

Depthwise separable Convolution

MobileNet 모델은 depthwise separable convolution을 기반으로 만들어졌습니다. Depthwise separable model은 factorized convolution의 한 방식으로 기본적인 convolution을 depthwise convolution과 $1 \times 1$ convolution인 pointwise convolution으로 분해한 것입니다.

Standard Convolution

기본적인 convolution은 입력값을 필터를 적용함과 동시에 합쳐서 단 하나의 단계로 출력값으로 변환합니다. 우리가 만약 입력 feature map을 $D_F \times D_F \times M$ 으로 출력 feature map을 $D_F \times D_F \times N$ 으로 표현한다면 기본 convolution layer의 kernel 크기를 다음과 같이 표현할 수 있습니다.

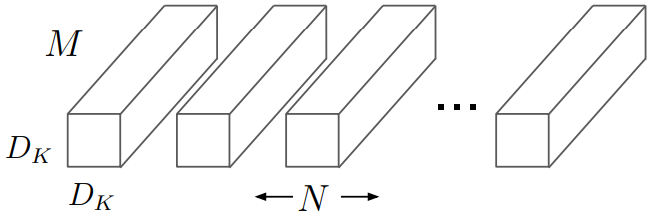
Standard Convolutional Filters

위의 이미지에서 보인것 처럼, 기본 convolutional layer는 필터크기가 $D_K \times D_K \times M \times N$ 으로 표현 될 수 있습니다. 여기서 $D_K$ 는 filter kernel의 크기, $M$ 는 input Channel의 크기. $N$ 는 output Channel의 크기입니다..

Kernel의 크기와 입력값의 크기를 알고 있다면, 우리는 기본적인 convolutional layer의 연산량을 대략적으로 계산 할 수 있는데, 그 수식은 아레와 같습니다.

$D_K \times D_K \times M \times N \times D_F \times D_F$

Depthwise Separable convolution

기본적인 Convolution과는 다르게 depthwise separable convolution은 두개의 레이어로 분류할수 있습니다.

필터를 위한 Depthwise convolution
하나로 합치기 위한 Pointwise convolution

Depthwise convolution은 depthwise separable convolution에서 필터하기 위한 단계입니다. 이 단계에서 하나의 필터가 하나의 입력 Channel에서 적용됩니다. 아래의 이미지와 같이, kernel 크기는 $D_K \times D_K \times M \times 1$ 가 됩니다.

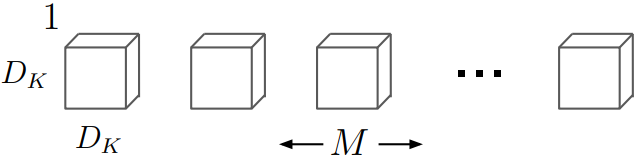
Depthwise convolution filter

Depthwise convolution 필터의 연산량은 기본 convolution layer보다 비교했을때 매우 작습니다. 왜냐하면 모든 입력값들을 필터하기 위한 추가적인 parameter가 필요 없기 때문입니다. 연산량을 수식으로 표현한다면 아래와 같습니다.

$D_K \times D_K \times M \times D_F \times D_F$

Pointwise convolution은 depthwise separable convolution에서 필터된 값들을 합치는 단계입니다. 이 단계에서 $1 \times 1$ convolution이 모든 필터 값들을 합치는데 사용됩니다. 이때 kernel 크기는 $1 \times 1 \times M \times N$ 입니다

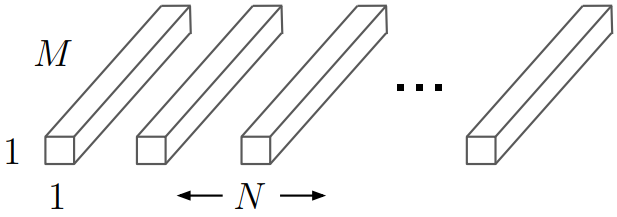
Pointwise convolution filter

Pointwise convolution 필터의 연산량은 입력값과 출력값에 비례합니다. 하지만 Kernel 크기와는 무관합니다. 이때의 연산량은 아래의 수식으로 표현됩니다.

$M \times N \times D_F \times D_F$

Depthwise convolution과 pointwise convolution의 합을 구하면, depthwise separable convolution의 총 연산량을 구할 수 있습니다. 이때의 합은 아래의 수식으로 표현됩니다.

$D_K \times D_K \times M \times D_F \times D_F + M \times N \times D_F \times D_F$

Reduction in Computation.

연산량을 계산한 두 개의 식으로 부터 우리는 depthwise separable convolution을 사용할때와 standard convolution을 사용할때의 연산량을 비교할 수 있습니다. 이를 통해서 depthwise separable convolution이 얼마만큼 연산을 줄일 수 있는지 계산 하게 되면,

$computaion ratio$

MobileNet의 Kernel 크기가 $3\times3$ 입니다. 그럼으로, MobileNet은 대략 8배에서 9배 정도로 연산을 적게 합니다.

Network Structure and Training

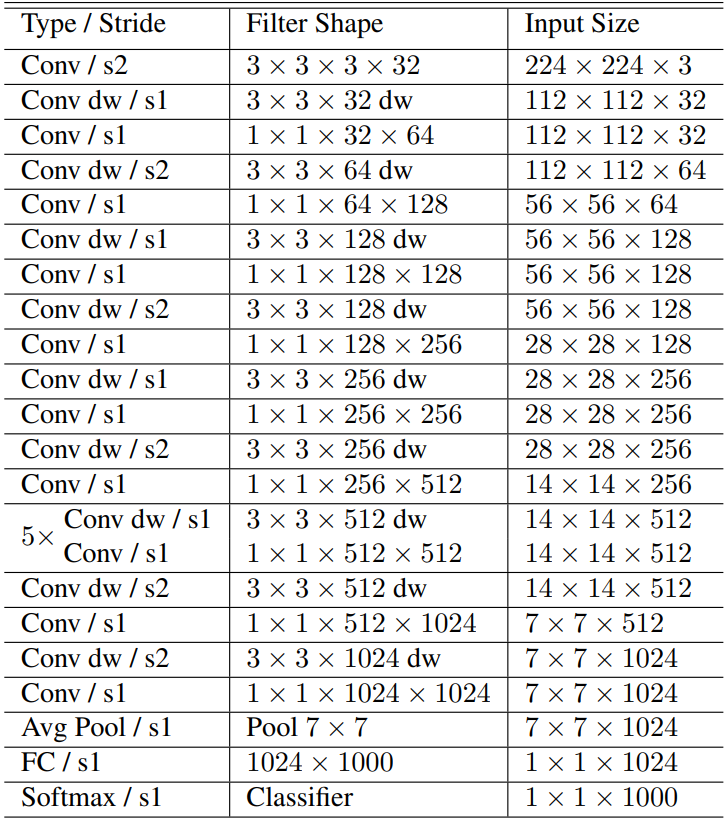
mobilenet structure

MobileNet의 기본적 구조는 depthwise separable convolution을 기반으로 만들어졌습니다. 이때 가장 첫번째 layer만은 Full convolution을 사용합니다. 마지막의 fully connected layer를 제외한 모든 layer는 batch normalization과 ReLU non-lineality가 뒤따릅니다. 마지막 레이어인 Funnly Connected layer는 softmax layer를 사용합니다. Downsamping은 depthwise convolution의 stride를 바꾸는 것으로 합니다. 가장 첫번째 layer인 standard convolution layer에서의 downsampling도 stride를 바꾸는 것으로 대신합니다. 마지막 average pooling은 공간 해상도를 1로 바꾸어 마지막 layer인 fully convolutional layer의 입력방식에 맞추어 줍니다. depthwise convolution과 pointwise convolution을 다른 layer라고 생각했을때 MobileNet은 총 28개의 layer로 이루어 져있습니다.

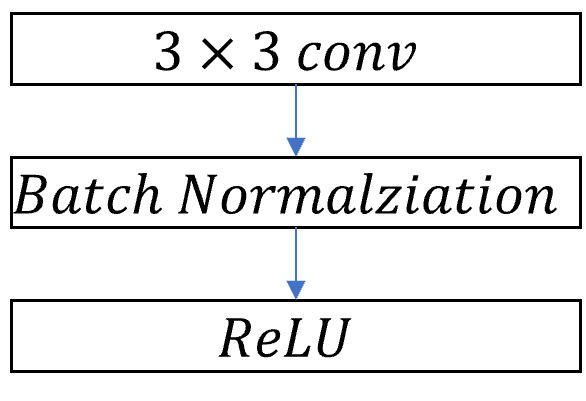
Standard Convolutional layer	Depthwise Separable Convolutional Layer

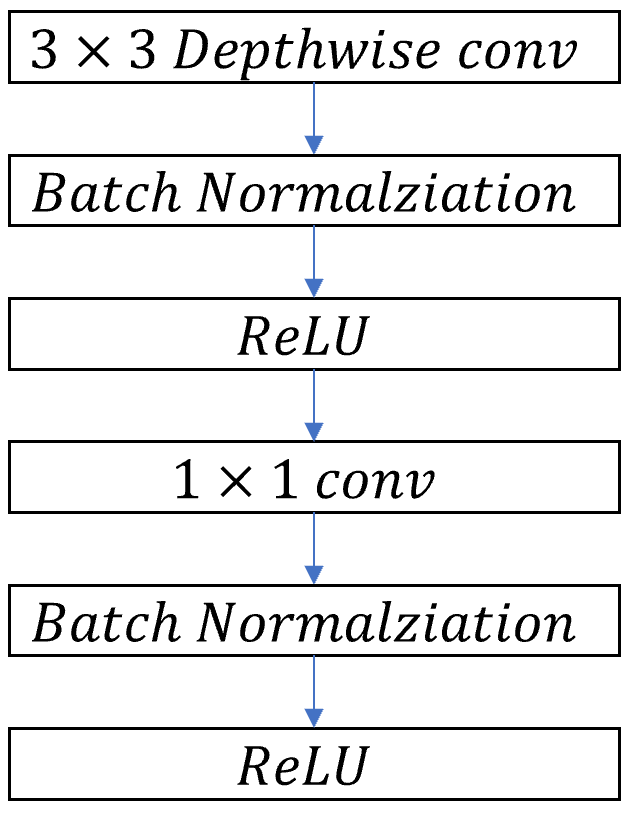위의 이미지는 standard convolution layer와 depthwiese separable convolutional layer의 차이점을 보여줍니다. 위에서 표현한것 처럼 standard convolution은 한단계에서 모든 것을 연산합니다. 반면, depthwise seaprable convolution은 depthwise separable convolution을 통해서 channel별로 filter하고 pointwise convolution을 통해서 입력값들을 합쳐 출력값으로 변환합니다.

효율적인 신경망은 단순히 Mult-Adds갯수만으로 정의되지 않습니다. 하지만 얼마나 효율적인 연산으로 실행되는 지가 더 중요합니다. 예를 들어서 sparse matrix연산은 dense matrix 연산보다 항상 빠르지 않습니다.

Width Multiplier: Thinner Models

MobileNet구조는 이미 작고 연산이 빠릅니다. 하지만 많은 경우, 특별한 경우나 어플리케이션의 경우 더 작은 모델을 원하거나 더 빠른 모델을 원하는 경우가 많습니다. 이때 작은 모델과 연산량이 적은 모델을 만들기 위해서 저자는 width multiplier를 소개합니다.

Width multiplier $alpha$ 의 역할은 전체적으로 신경망의 구조는 얇게 만들어 줍니다. 하나의 레이어가 주어졌을때, width multiplier를 사용하면, 입력값의 크기인 M이 $alpha$ 로 변하게 되고, 출력값도 비슷하게 적용이 됩니다. 이 경우 총 연산량은 아래와 같이 변하게 됩니다.

$Width Multiplier$

여기서 $alpha$ 의 값은 0과 1 사이의 값이 됩니다. $alpha=1$ 일때, baseline MobileNet이고, $alpha<1$ , reduced MobileNets입니다..

Width Multiplier사용할때, 연산량이 width multiplier의 제곱에 비례하게 줄어듭니다.

Resolution Multiplier: Reduced Representation

Resolution Mutliplier $rho$ 는 입력 이미지와 중간 표현값들에게 적용되어 연산량을 줄여줍니다.

Width multiplier $alpha$ 와 resolution Multiplier $rho$ 를 동시에 적용시킨다면, depthwise separable convolutional layer의 연산량을 아래와 같이 표현할수 있습니다.

$Resolution Multiplier and Width Mutliplier$

Experiment

Depthwise separable convolution의 효과와 layer의 갯수를 줄이는 것 대신에 network의 width를 줄이는 것의 효과

Model Choices

Depthwise separable convolution을 사용한 MobileNet과 Full convolution을 사용한 MobileNet의 비교.

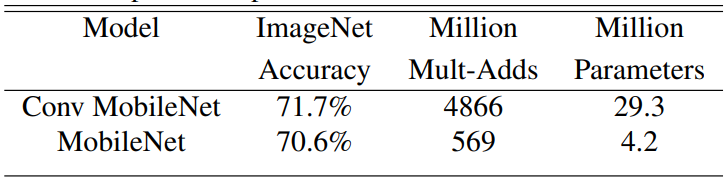
depthwise separable vs full convolution mobile net

위의 테이블을 확인한 결과, depthwise seaprable convolution을 사용한 결과 9배정도 연산이 줄어들었고 1% 정도의 정확도가 줄어들었다.

Width multiplier를 사용하는 얇은 모델과 더 적은 수의 layer를 사용하는 얕은 모델을 비교한다. 얕은 MobileNet을 만들기 위해서, 5개의 separable filter를 삭제했다. 이때의 feature map 크기는 $14 14 512$ 이다.

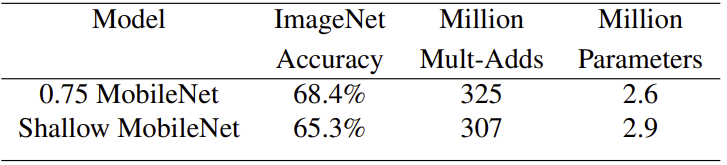
thin model vs shallow model

위의 표를 확인해 보면, 얇은 모델과 얕은 모델 모두 비슷한 연산량과 parameter 수를 가지고 있다. 하지만 얇은 모델이 얕은 모델에 비해서 3% 더 정확하다.

Model shrinking hyperparameters

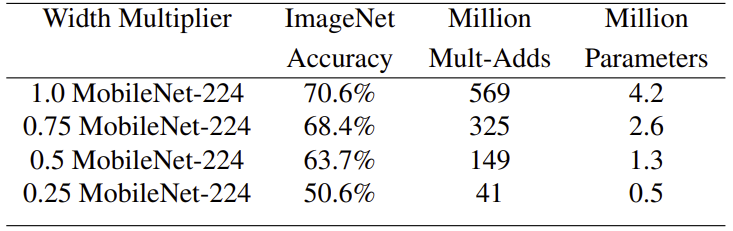
mobile net width multiplier comparison

Width Multiplier $alpha$ 를 이용한 MobileNet의 축소는 정확도와 연산량, 크기의 교환으로 이루어 진다. Width Mutliplier가 줄어들수록, 정확도도 부드럽게 줄어드는데, parameter의 수가 급격하게 작아지는 $alpha$ 일때 정확도는 급격하게 떨어진다. 이 때는 parameter의 수가 너무저어서 정확한 결과값을 찾기가 어려워진다.

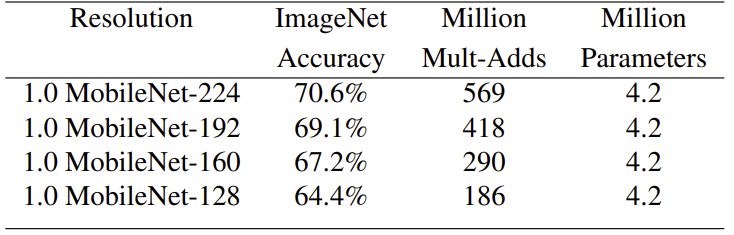
mobile net resolution mutliplier comparison

resolution multiplier $rho$ 를 이용한 MobileNet의 축소는 정확도와 연산량, 크기의 교환으로 이루어 진다. Resolution Mutliplier가 줄어들수록, 정확도도 부드럽게 줄어든다.

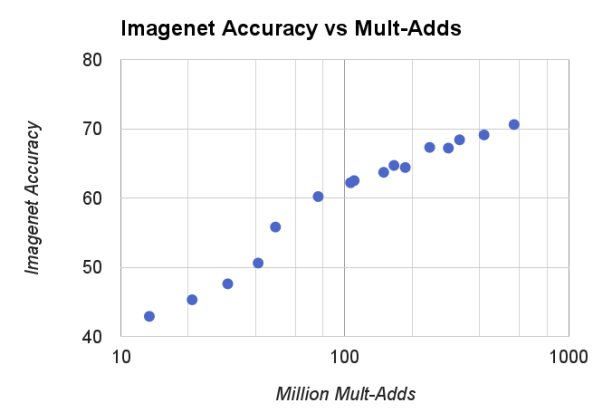
computation vs accuracy

위의 그래프를 확인해보면, Computational complexity에 비래해서 ImageNet benchmark값이 상승하는 것을 볼수 있다. 여기서 x축은 지수적으로 증가하는 것을 알아야한다.

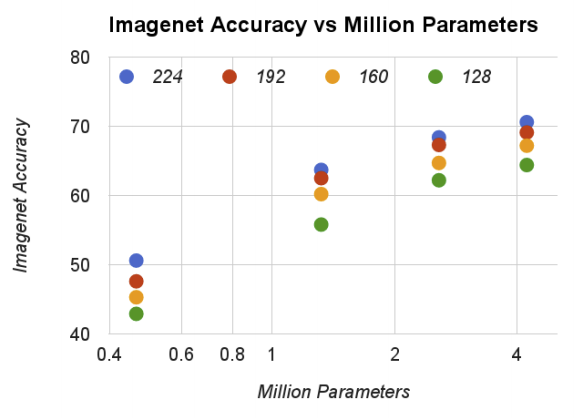
parameter vs accuracy

위의 그래프는 parameter의 개수과 정확도를 비교한 것이다. 여기서 parameter의 수가 높을 수록 정확도가 올라가는 것을 볼수 있다. 그리고 parameter의 수는 resolution multiplier와는 관계가 없는 것을 확인할 수 있다.

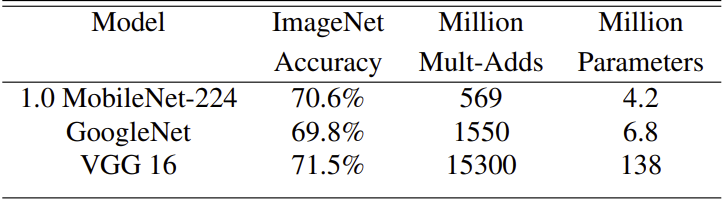
MobileNet vs popular models

MobileNet과 다른 유명한 인공신경망을 비교해보았다. MobileNet은 VGG16과 비슷한 정확도를 가지는데, 32배적은 parameter 수를 가지고 있고 27배 연산량이 작습니다. GoogleNet과 비교시, MobileNet이 1%정도 정확도가 높지만, 3배 정도 연산이 적고 1.5배정도 parameter 수가 적습니다.

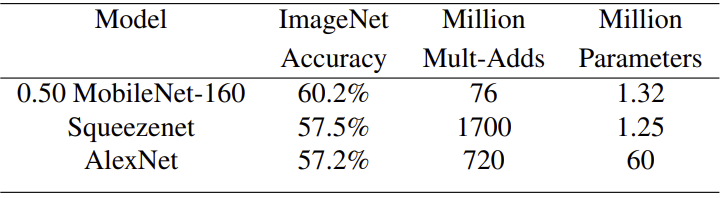
small mobile net vs popular models

Width Multiplier를 0.5를 사용하고 해상도를 $160 160$ 으로 줄인 MobileNet은 Squeezenet과 Alexnet에 비해서 확실하게 좋습니다. Squeezenet은 22베 많은 연산량에고 불구하고 3%정도 낮은 정확도를 보였고, AlexNet도 45배 많은 parameter에 9.4배 많은 연산량에도 불구하고 3%적은 정확도를 보였습니다.

About Artificial Intelligence

Different Kinds of Artifical Intelligence